Chapter 13 - Mathematics of Electron Spin
I. What is physical spin?
II. Dirac’s Theory of Electron Spin
III. The Group Mathematics of Spherical Rotation
IV. The magical CPT operations and spin
V. References
“A Positron is an Electron traveling backward in time”
- Richard Feynman
Dirac and others (see Eisele, 1960) [1] developed a theory for the spin of the
electron, which successfully predicted the positron (Anderson, 1922) and
correctly provided the experimental value of the spin as
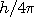 . Spin is
widely accepted as a quantum mechanical phenomenon, but a physical description
that provides an origin of spin has never been proposed. In other words,
before this book, no one knew how or why spin happens; it was a mystery of
quantum. Presenting a physical origin of spin, that agrees with quantum
theory, the Dirac Equation, and the electron wave-structure of the Space
Resonance theory, is the purpose of this Section.
. Spin is
widely accepted as a quantum mechanical phenomenon, but a physical description
that provides an origin of spin has never been proposed. In other words,
before this book, no one knew how or why spin happens; it was a mystery of
quantum. Presenting a physical origin of spin, that agrees with quantum
theory, the Dirac Equation, and the electron wave-structure of the Space
Resonance theory, is the purpose of this Section.
Dirac calculated spin of a particle in units of angular momentum, however the
mechanism is not like the rotary angular momentum of the Earth or a wheel,
because we are dealing with quantum phenomenon; something is different. The
value of spin is fixed - quantized - and independent of particle mass or
angular velocity. Spin is found to be a property of 3D space and related to
other properties of the electron's quantum wave structure. These spin- related
properties are called charge inversion, mirror or parity inversion, and time
inversion. They are operations on the wave functions of a particle, like
flipping a switch, to change between two states, such as + and - or up and
down. They are represented by the symbols
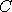 ,
,
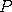 , and
, and
 . The special thing
about them is that three successive operations on a particle are found to
change the particle back to the beginning. This is written
. The special thing
about them is that three successive operations on a particle are found to
change the particle back to the beginning. This is written
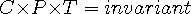 | (13.1) |
These operations are very simple and interesting so more will be written about them below. especially since no one knew why it happens that way before the WSM.
I. What is physical spin?
As discussed throughout this book, the electron is comprised of two spherical
scalar waves, one inward and one outward. A phase shift of the inward wave
occurs in the wave-center region near where
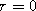 , and spin appears as a
required rotation of the inward wave in order to become the outward wave.
This requirement is a property of 3D space termed spherical rotation. To
transform the inward wave to an outward wave and obtain the out-wave with
proper phase relations requires phase shifts of the in-wave at the center.
These phase shifts produce a spin value of
, and spin appears as a
required rotation of the inward wave in order to become the outward wave.
This requirement is a property of 3D space termed spherical rotation. To
transform the inward wave to an outward wave and obtain the out-wave with
proper phase relations requires phase shifts of the in-wave at the center.
These phase shifts produce a spin value of
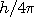 in the entire wave
structure as seen below. Because spin is the result of required wave phase
shifts, a property of 3D space, spin has the same value for all charged
particles independent of other particle properties.
in the entire wave
structure as seen below. Because spin is the result of required wave phase
shifts, a property of 3D space, spin has the same value for all charged
particles independent of other particle properties.
Before the WSM, that fact that spin in say a heavy proton, is the same as in a small mass electron has been a mystery. If one uses a discrete particle model (as in the current Standard Model) conventional physicists calculate that a heavy proton should have a much larger angular momentum (spin) than a light electron. They imagine spinning particles like toy tops - the mistaken result of the discrete particle model. Now the WSM shows that the origin of spin is a property of the 3D space medium. There is no mystery; all particles are in the same quantum-wave space and all have the same spin.
Rotation in space has requirements: Any mechanism that rotates the in-wave phase (creating the quantum spin) must not destroy the continuity of the space. The curvilinear coordinates of the space near the particle must participate in the motion of the particle. Fortunately, 3D space has a unique way to do this termed spherical rotation. According to the group theory mathematics of 3D space, continuity is described by stating that the allowed motions must be represented by the SU(2) group algebra, which concerns simply connected geometries.
Spherical rotation is an astonishing property of 3D space. It permits an object structured of space to rotate about any axis without rupturing or twisting-up the coordinates of space. Space is flexed but after two turns, space regains its original configuration. This property allows the electron to retain spherical symmetry while imparting a quantized "spin" along any arbitrary axis. The inward wave converges to the center, undergoes phase shifts to become the outward wave. The in-waves and out-waves continuously go through the phase shift process; the spin is a property of the entire wave structure that exists in the 3D space medium.
The required phase shift is a 720° rotation that changes inward wave
amplitudes to become those of the outward wave. There are only two possible
directions of rotation, CW or CCW. One direction produces an electron with spin
of 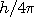 ,
and the other is the positron with spin of
,
and the other is the positron with spin of
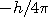 .
.
II. Dirac’s Theory of Electron Spin
The physical nature and cause of electron spin has been sought for 75 years ever since Nobel laureate Paul Dirac made a calculation of spin in 1926. His theoretical work predicted the positron, found five years later by C. D. Anderson. Only recently has the physical origin of spin seen to be a simple result of the wave structure of matter.
Dirac sought to find a relation between quantum theory and the conservation of energy in special relativity given by,
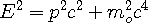 | (13.2) |
He speculated that this energy equation might be converted to a quantum equation
in the usual way, in which energy
 and momentum
and momentum
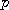 are replaced by differential calculus operators,
are replaced by differential calculus operators,
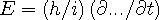 and
and
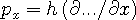 ... etc
... etc
| (13.3) |
He hoped to find the quantum differential wave equation of the particle. Unfortunately, Eqn (13.2) uses squared terms and Eqn (13.3) cannot. Dirac cleverly decided to use the terms of Eqn. (13.2) without squares, by writing a matrix equation,
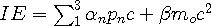 | (13.4) |
Where 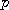 is the
electron’s momentum and
is the
electron’s momentum and 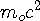 is its energy. Dirac proposed that if
is its energy. Dirac proposed that if
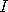 , the identity operator,
and
, the identity operator,
and  and
and 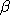 were 4-vector matrices then Eqn. (13.4) would work. He obtained the famous Dirac
Equation by combining Eqns. (13.3) and (13.4) to get,
were 4-vector matrices then Eqn. (13.4) would work. He obtained the famous Dirac
Equation by combining Eqns. (13.3) and (13.4) to get,
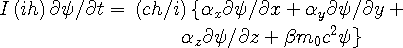 | (13.5) |
In general, 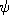 is a 4-vector:
is a 4-vector: ![\psi=\left[\psi_{1},\psi_{2},\psi_{3},\psi_{4}\right]](spin-qed_math/math0009.gif) .
For the electron, this reduces to:
.
For the electron, this reduces to:
![\psi=\left[0,1,\psi_{3}\left(E,p\right),\psi_{4}\left(E,p\right)\right]](spin-qed_math/math0010.gif) a vector with only two variables in it. Dirac then realized that for an
electron only two wave functions,
a vector with only two variables in it. Dirac then realized that for an
electron only two wave functions, 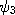 and
and 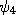 ,
were needed since the other two terms are constants. Solving for the values of
these two wave functions, he predicted an electron and a positron with energy and spin,
,
were needed since the other two terms are constants. Solving for the values of
these two wave functions, he predicted an electron and a positron with energy and spin,
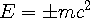 and
and
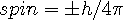
| (13.6) |
The positron was discovered five years later by Anderson (1931) and led to Dirac’s Nobel prize.
Dirac simplified the matrix algebra by introducing 2-vectors (number
pairs), which he termed spinors
(=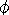 )
that replace the 4-vectors. The spin 2-matrices
(=
)
that replace the 4-vectors. The spin 2-matrices
(= ),
which operate on the 2-vectors, were defined as follows,
),
which operate on the 2-vectors, were defined as follows,
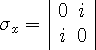
|
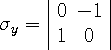
|
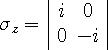
|
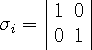
| (13.7) |
Thus Dirac had created a two-number algebra to describe particles instead of our common single number algebra. This spinor algebra, while eminently successful, was entirely theoretical and gave no hint of the physical structure of the electron.
The origin of the electron’s spin. Spin is an example of the depth and universality of the Wave Structure of Matter. It is now seen below that the inward-outward quantum waves are the physical structures that correspond to the Dirac spinors. The physical spinors (2-vectors) of the electron or any charged particle, are as follows,
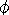
| spinors are: |
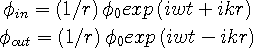
| (13.8) |
where 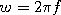 and
and
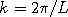 = wave number. The
discovery that spin (a real measurable momentum) is a result of rotation
of the spherical quantum waves also shows that quantum waves are indeed
real. A readable simple description of the algebra of the Dirac Equation
is given in Eisele (1960). [1] Battey-Pratt et al (1986) show
spin in more detail. [2]
= wave number. The
discovery that spin (a real measurable momentum) is a result of rotation
of the spherical quantum waves also shows that quantum waves are indeed
real. A readable simple description of the algebra of the Dirac Equation
is given in Eisele (1960). [1] Battey-Pratt et al (1986) show
spin in more detail. [2]
III. The Group Mathematics of Spherical Rotation
Geometric Requirements of Electron Spin. Electrons cannot spin separately from the space of which they are structured and connected. If they spin freely as discrete particles, the connected space would twist itself up; that is, the coordinate lines of space would stretch and wrap around one another. The structure of space would be torn or ripped; or, one part of space must slide past another section of space. This concept is illogical and meaningless. This is why spin is purely a quantum wave property of matter.
If you accept the reasonable philosophical view that discontinuities or "tearing” of space is unacceptable, then you have to postulate, in the jargon of mathematical groups, that the groups describing particle motion are simply connected and compact. In this case the motion in the space-continuum will be cyclic and the configuration of space can repeatedly return to an initial state. This motion is termed Spherical rotation, which is a unique mathematical property of 3D space; that is, a portion of space rotates and returns identically to an earlier state after exactly two turns. This unusual motion was described in Scientific American by Rebbi (1979) [3] and in the book Gravitation by Misner, et al (1973) [4] though they did not know at that time, its connection with spin. Its recognition as the basis of spin is a result of the WSM shown below.
Group theory of spin. What are the geometric requirements on the spin of a particle wave, which does not destroy the continuity of the space? The curvilinear coordinates of the space near the particle wave-center must participate in the motion of the particle waves. That a compact simply-connected group represents the allowed motions satisfies this requirement according to the group theory of 3D space. The most elementary such group for the motion of a particle wave-center with spherical symmetry is named SU(2). This group provides all the necessary properties of spin for charged particles, such as the electron.
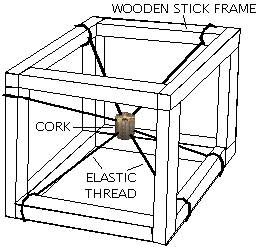
| Figure 13.1 SUPPORTING FRAME MADE OF STICKS - A Model of Spherical Rotation. This apparatuc is easily made out of a few sticks, a cork and six rubber bands. The cork can be rotated (taking care not to knot up the rubber bands) continously without entangling the rubber bands! The cork and the bands will return to their initial configuration every two turns. This demonstrates a little known variety of rotation. It has application to particle theory because the spherical rotation does not destroy continuity of space. |
Understanding Spherical Rotation. A ball held by threads attached to a frame as in Figure 13.1, can model this seldom-studied motion. The threads represent the coordinates of the space and the rotating ball represents a property of the space at the center of a charged particle composed of converging and diverging quantum waves. The ball can be turned about any given axis starting from any initial position. If the ball is rotated indefinitely it will be found that after every two rotations the system returns to its original configuration.
Inversion of spin axis. In the traditional analysis of ordinary rotating objects, it is usual to assume that inverting the axis of spin is identical to reversing the spin. However, if the object is an electron, whose waves are connected to space as part of the space around it, this ceases to be true. A careful distinction must be made between the reversal and the inversion of particle spin. This distinction provides insight to one of the most fundamental properties of particles.
To reverse the spin axis, reverse time by changing
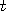 to
to
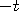 or reverse the angular velocity,
or reverse the angular velocity,
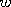 to
to
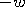 .
Either is equivalent to exchanging the outgoing spherical wave of an
electron with the incoming wave. Then the spinor changes as follows:
.
Either is equivalent to exchanging the outgoing spherical wave of an
electron with the incoming wave. Then the spinor changes as follows:
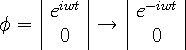
|
To invert the spin axis of the structure of the particle, it is necessary to turn the structure about one of the two axes perpendicular to the z spin axis, for example the y-axis. Then the inverted spin state is produced by using the inversion matrix operator, so
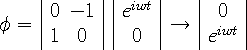
|
The results are not the same, so inversion and reversal are not the same. The difference between these two operations is characteristic of the quantum nature of the electron particle structure. They are different from our human-sized view of rotating objects.
Each configuration of the electron’s wave-center (like a spherically rotating
ball) can be represented by a point on a Euclidean 4-D hypersphere that is
also the space of the SU(2) mathematics group. Any operator that will
transform one vector into another position can represent a spherical rotation.
It is usual to assign the hypersphere a unit radius. Then the rotations of
the ball can be described by the mathematics of the SU(2) group. It is also
convenient to place the center of the unit hypersphere at the origin and let
the vector 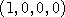 represent an initial configuration of the ball or electron.
Any other configuration is often chosen with the symbols
represent an initial configuration of the ball or electron.
Any other configuration is often chosen with the symbols
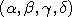 .
Then
.
Then 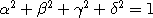 .
.
A common representation for the hypersphere vectors is the quaternion notation,
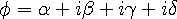
|
Battey-Pratt and Racey (1986) [2] showed that the 4x4 quaternion operator is equivalent to a 2x2 operator,
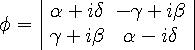
|
Where the matrix elements are now complex numbers that are combinations of
1, i, or 0. You can see that the determinant of this is also:
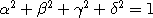 ,
as above. The spinor (operand) form of
,
as above. The spinor (operand) form of
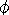 is,
is,
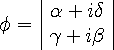
|
This is the notation of the Spinors invented by Dirac to represent the electron configuration, as shown in Table 13.1. They also represent rotations in the spherical mode that are members of the closed uni-modular SU (2) group.
| Table 13.1: Properties of Spherical Rotation for an electron in the SU(2) Representation |
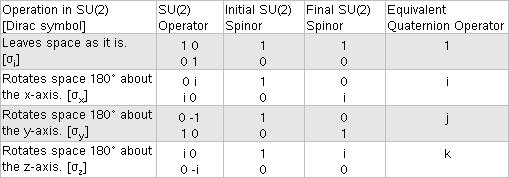
|
For example, the spherical quantum waves in space are rotated 180° about the
z-axis by the operator 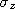 .
If there is continuous rotation of the quantum wave in space with angular velocity
.
If there is continuous rotation of the quantum wave in space with angular velocity
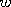 , the spinor
, the spinor
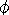 is represented by
is represented by
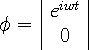
|
How Spin Arises from the Wave Structure of the Electron. As previously
described in this book, the inward spherical quantum wave of the space-resonance
is transformed into an outward spherical wave when it arrives at the wave-center.
The only way that Nature allows this to happen in the geometry of 3D space is by
a spherical rotation, or phase shift of the spherical in-wave, using the SU(2)
group math above. The amount of phase shift required by the geometry of 3D space
is two turns per wavelength, which results in a continuous spin of
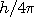 .
This result is easy to calculate. Try it! This geometric mechanism of phase
shift in an electron has an analogy in the required phase shift of light when
it reflects at a mirror; it must shift an angle
.
This result is easy to calculate. Try it! This geometric mechanism of phase
shift in an electron has an analogy in the required phase shift of light when
it reflects at a mirror; it must shift an angle
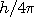 so that the impinging wave is in phase with the reflected wave.
so that the impinging wave is in phase with the reflected wave.
The required phase shift of the inward wave can happen in either of two
rotary directions denoted 'CW' or 'CCW'. Thus there are two possible ways
to shift the inward waves. One way of rotation produces an electron while
the other way is a positron. The in/out wave pair of the electron is
the mirror image of the positron pair. The resulting added angular momentum
due to phase shift is either
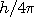 or
or
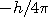 .
This is the origin of quantum spin.
.
This is the origin of quantum spin.
IV. The magical CPT operations and spin
What did Feynman mean when he said: "A Positron is an Electron traveling
backward in time"? As a mathematician he was speaking of the way you
deal with electrons and positrons. Mathematically: To change the direction
of time, you replace a
'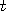 '
with a
'
'
with a
'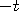 ':
termed the T operation. This also appears to change the electron to a
positron because it changes all the wave directions from IN to OUT and
vice-versa. This is one of three operations on electrons called CPT
operations described below.
':
termed the T operation. This also appears to change the electron to a
positron because it changes all the wave directions from IN to OUT and
vice-versa. This is one of three operations on electrons called CPT
operations described below.
CPT Operations. CPT means three instructions as follows: Using a particle of interest, perform the C operation on its structure, then the P operation, and then the T operation. Classical theorists knew that after all three operations the particle ends up un-changed, but before the WSM they didn’t know why. To understand what CPT is all about, we must use the equations of an electron and a positron. They are Eqns. [12.2 and 12.3] in Chapter 12, solutions of Principle I - the wave equation. They are the only two possible spherical wave solutions:
Outward wave: 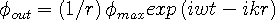
| (12.2) |
Inward wave: 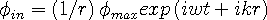
| (12.3) |
Where 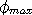 is a scalar wave amplitude, frequency
is a scalar wave amplitude, frequency
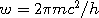 ,
,
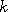 = wave number.
The physical dimension
= wave number.
The physical dimension  is the radius of the spherical waves, from a wave center. The wave centers are the apparent location of
the 'particles'. The waves are continually diverging and converging as drawn in Figure 2.1. The wave
pair forms a resonance in space with a wave-center that we observe as the ‘particle’ location.
is the radius of the spherical waves, from a wave center. The wave centers are the apparent location of
the 'particles'. The waves are continually diverging and converging as drawn in Figure 2.1. The wave
pair forms a resonance in space with a wave-center that we observe as the ‘particle’ location.
Thoughts for the reader: By the way, have you noticed yet that Nature makes two of everything? Is Nature a binary computer? Is Nature a synonym for 3D space?
Waves of the electron-positron. These two waves can be combined in only two ways to form the electron-positron. These are combinations of the in- and out- spherical waves:
Electron = 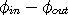 with CW spin with CW spin
| (12.3) |
Positron = 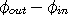 with CCW spin with CCW spin
| (12.3) |
The in-waves reverse their direction at the center in one of two ways to become out-waves. This reversal is expressed mathematically by CW and CCW that are rotation (spin) operators on the waves. See the spin operators above. You can easily show that these two equations contain the CPT properties.
Spin-axis operations. Using the exponential wave solutions for the
electron shown above, Eqns 12.2 and 12.3, you can reverse the spin axis, by
reversing time (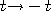 )
or by reversing the angular velocity
(
)
or by reversing the angular velocity
(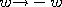 ). Both are
equivalent to switching the outgoing spherical wave of an electron with
the incoming wave. You may quickly check the particles with Eqns. [12.4
and 12.5] above. Another change is inverting the spin state; produced
by the inversion matrix operating on the spinor. But this does not change
the direction of the in/out waves.
). Both are
equivalent to switching the outgoing spherical wave of an electron with
the incoming wave. You may quickly check the particles with Eqns. [12.4
and 12.5] above. Another change is inverting the spin state; produced
by the inversion matrix operating on the spinor. But this does not change
the direction of the in/out waves.
The CPT operations are very simple. To perform a Time
inversion, change 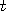 to
to 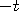 ,
which converts the positron into an electron. To perform a mirror inversion
(Parity), imagine that the waves are viewed in a mirror; a positron
is a mirror image of the electron. To change a particle to an anti-particle
(Charge inversion), switch the in-waves and the out-waves, and the
spin. The successive C, P, and T inversions return
an electron to its initial state proving that the CPT rule is a property of
the wave structure.
,
which converts the positron into an electron. To perform a mirror inversion
(Parity), imagine that the waves are viewed in a mirror; a positron
is a mirror image of the electron. To change a particle to an anti-particle
(Charge inversion), switch the in-waves and the out-waves, and the
spin. The successive C, P, and T inversions return
an electron to its initial state proving that the CPT rule is a property of
the wave structure.
Protons are different than positrons. Consider why a proton is distinct from a positron. Both of them have identical charge waves, i.e. identical in-waves and out-waves, but the difference is at the wave center, as follows:
The positron in-wave arrives at the center, undergoes spherical rotation to change phase at the center, say CW (a rotary direction of an object) and leaves as an out-wave. But the proton is different because at the center the waves are part of a more massive resonance at a higher frequency,because the space is very dense at the center. Because of this dense central space the proton wave-center is not a mirror image of the electron’s wave center; so the proton cannot annihilate with an electron. Nor can a positron annihilate with an anti-proton.
Compare the electron and the positron: One has CW phase shift at the center, the other has CCW shift. They are like the left hand and the right hand. One is the mirror image of the other. The amplitudes are exactly opposite so they can annihilate each other if super-imposed!
You can prove this: Go to the two equations [12.4 and 12.5] that are the in/out waves of the electron or positron. Choose the combination that forms an electron. Then perform a mirror image change (This is termed P, the parity operation) by switching + and - signs. This turns the electron into the positron. You can make the positron turn into an electron in the opposite way!
To further convince yourself, perform the C charge operation on the equations. (Switch the in-waves and the out-waves, and the spin). Lo! The electron becomes a positron going backward in time! This is the proof of what Feynman said, but he only knew it from experimental observation not as a wave structure, that you the reader, now understand. You now know more than Feynman did! The electron does not really go backward in time (only in Hollywood) because by switching the +t and -t terms you only exchanged the in- out-waves that make the electron become a positron.
Feynman often used the math of in-waves and out-waves but he never gave up the concept of the discrete point particle. His colleague at Caltech, Carver Meade, admired him immensely but wrote (2000) in his book, on the particle concept, "That was Feynman’s biggest mistake." [5]
Conclusions from Spin. Following the previous chapters of this book, the origin of spin completes the description of the electron. All properties of the electron can now be derived from the space-resonance structure (WSM) that match the experimental observations of the electron that are contained in the half-dozen empirical natural laws.
Spin and Spherical rotation can occur only in 3D space, not 4D,
5D, etc. This is a geometric fact. Accordingly we must conclude
that matter as we know it, indeed the whole Universe, depends on
the existence of this 3D geometric property. If 3D spherical
rotation and spin did not exist we could not exist! We barely
understand Nature and its raw material space but we do know that
Nature chooses binary objects and the properties of space are the
origin of matter. The laws of nature are attributes of the
underlying quantum space that is the wave medium. Thus the binary
electron properties depend on the structure of space, not on the
type of particle. This is why spin and charge have only one pair
of  values for all particles.
values for all particles.
V. References
| [1] | John A. Eisele, Modern Quantum Mechanics with Elementary Particle Physics, (Wiley, NY, 1960). |
| [2] | E. Batty-Pratt and T. Racey, "Geometric Model for Fundamental Particles", Int. J. Theor. Phys.19, pp. 437-475 (1980). [They recognized that electron spin was a geometric property of space and could exist in a spherical space structure.] |
| [3] | Rebbi, Claudio, "Solitons", Sci. Am. 240(2), pp. 92-116 (Feb 1979). |
| [4] | Charles Misner, Kip Thorne, and John Wheeler, Gravitation, p. 1149, (W.H. Freeman Co. San Francisco, 1973). [Describes a classic study of 'spherical rotation'.] |
| [5] | Carver Meade, Collective Electrodynamics, (MIT Press, 1999). |