1D Animation and Implementation Details of in-, out- and Resulting Scalar Waves - February 23, 2010

Steven Dufresne

Abstract

This is a 1 dimensonal look at what the in- and out-waves for an electron look like. Note that this is for a single electron and so does not show any resonance or doppler effects. As it is demonstrating the in- and out-waves, no spherical rotation is done at the electron center. It's more for giving an idea of how the in- and out-waves combine to form a scalar standing wave and some idea of the amplitudes and how they change with distance from the electron's wave center.

I. The animation

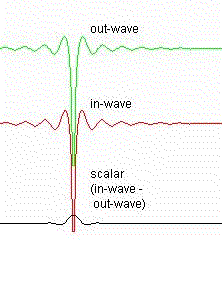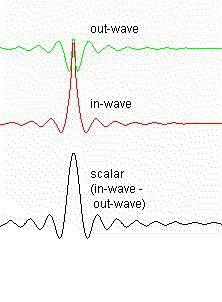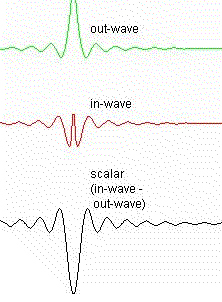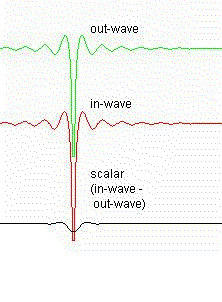
in-wave formula in trig. form: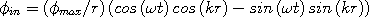
$\phi_{in}=\left(\phi_{max}/r\right)\left(cos\left({\omega}t\right)cos\left(kr\right)-sin\left({\omega}t\right)sin\left(kr\right)\right)$
Converted from: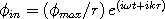
$\phi_{in}=\left(\phi_{max}/r\right)exp\left(i{\omega}t+ikr\right)$

out-wave formula in trig. form: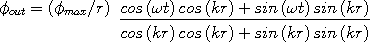
$\phi_{out}=\left(\phi_{max}/r\right)&\underline{cos\left({\omega}t\right)cos\left(kr\right)+sin\left({\omega}t\right)sin\left(kr\right)}\nonumber\\&cos\left(kr\right)cos\left(kr\right)+sin\left(kr\right)sin\left(kr\right)\nonumber$
Converted from: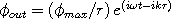
$\phi_{out}=\left(\phi_{max}/r\right)exp\left(i{\omega}t-ikr\right)$

scalar wave formula used for graph:
in-wave - out-wave or 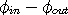$\phi_{in}-\phi_{out}$

II. How the out-wave equation was converted from exponential to trig. form

We start with the equation for the out-wave in exponent form:

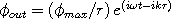$\phi_{out}=\left(\phi_{max}/r\right)e^{\left(i{\omega}t-ikr\right)}$

(1)

Break it into two exponents, each with their own imaginary number, i.

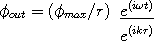$\phi_{out}=\left(\phi_{max}/r\right)&\underline{e^{\left(i{\omega}t\right)}}\nonumber\\&e^{\left(ikr\right)}\nonumber$

(2)

Convert this to cis form.

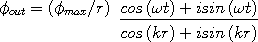$\phi_{out}=\left(\phi_{max}/r\right)&\underline{cos\left({\omega}t\right)+isin\left({\omega}t\right)}\nonumber\\&cos\left(kr\right)+isin\left(kr\right)\nonumber$

(3)

Multiply by the conjugate of the denominator.

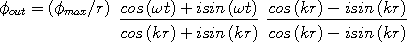$\phi_{out}=\left(\phi_{max}/r\right)&\underline{cos\left({\omega}t\right)+isin\left({\omega}t\right)}&\underline{cos\left(kr\right)-isin\left(kr\right)}\nonumber\\&cos\left(kr\right)+isin\left(kr\right)&cos\left(kr\right)-isin\left(kr\right)\nonumber$

(4)

Multiply out.

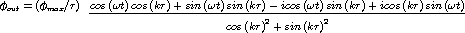$\phi_{out}=\left(\phi_{max}/r\right)&\underline{cos\left({\omega}t\right)cos\left(kr\right)+sin\left({\omega}t\right)sin\left(kr\right)-icos\left({\omega}t\right)sin\left(kr\right)+icos\left(kr\right)sin\left({\omega}t\right)}\nonumber\\&cos\left(kr\right)^2+sin\left(kr\right)^2\nonumber$

(5)

Rearrange as a complex number (step not shown) and throw away the imaginary part to get the final result.

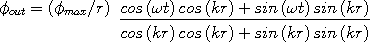$\phi_{out}=\left(\phi_{max}/r\right)&\underline{cos\left({\omega}t\right)cos\left(kr\right)+sin\left({\omega}t\right)sin\left(kr\right)}\nonumber\\&cos\left(kr\right)cos\left(kr\right)+sin\left(kr\right)sin\left(kr\right)\nonumber$

(6)

III. How the in-wave equation was converted from exponential to trig. form

We start with the equation for the in-wave in exponent form:

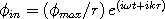$\phi_{in}=\left(\phi_{max}/r\right)exp\left(i{\omega}t+ikr\right)$

(7)

Break it into two exponents, each with their own imaginary number, i.

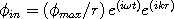$\phi_{in}=\left(\phi_{max}/r\right)e^{\left(i{\omega}t\right)}e^{\left(ikr\right)}$

(8)

Convert this to cis form.

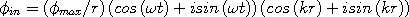$\phi_{in}=\left(\phi_{max}/r\right)\left(cos\left({\omega}t\right)+isin\left({\omega}t\right)\right)\left(cos\left(kr\right)+isin\left(kr\right)\right)$

(9)

Multiply out.

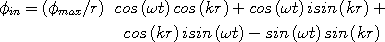$\phi_{in}=\left(\phi_{max}/r\right)&cos\left({\omega}t\right)cos\left(kr\right)+cos\left({\omega}t\right)isin\left(kr\right)+\nonumber\\&cos\left(kr\right)isin\left({\omega}t\right)-sin\left({\omega}t\right)sin\left(kr\right)\nonumber$

(10)

Throw away the imaginary parts to get the final result.

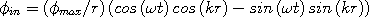$\phi_{in}=\left(\phi_{max}/r\right)\left(cos\left({\omega}t\right)cos\left(kr\right)-sin\left({\omega}t\right)sin\left(kr\right)\right)$

(11)

IV. Snippets from the Java code

The above animation is an animated GIF but was produced using a java program. The program would pause for a short period of time every 6th wave iteration, long enough for a snapshot to be captured. The snapshots were then combined into one animated GIF file for easy embedding on webpages.

Here are some snippets from the java program. First some declarations...

   int spacelen = 400;               // the width in pixels that the waves will be in
   int wavecenterloc;                // wave center location in space, for 1/r calculations

   double pi;
   double lambda = 2.4263102175e-12; // units - m, Compton wavelength
   double k = 2.589604676e12;        // units - (1/m), (2xpi)/lambda
   double w = 7.763439511e20;        // units - radians/s, (2xpixc)/lambda = kc
   double c = 299792458;             // units - m/s
   double t = 3.5e-18;               // units - s
   double dt = 1e-22;                // delta t, added to t each time
   double amp_max = 1e-12;           // maximum amplitude
...
   pi = Math.PI;
...

amp_max is 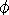_max in the equations above. It wasn't know what value should be used for amp_max so one was chosen that resulted in amplitudes that worked well with the animation. It is to scale though.

The following happens once for each iteration of the waveforms.

   t+=dt;
   draw_space(backg);

And here's the entire draw_space() routine that draws one iteration of the three waveforms.

   void draw_space(Graphics g) {
      int x, first = 1;
      int base_y = 100;
      double r;
      double amp_scalar;
      int amp_scalar_y, amp_scalar_yprev;
      double amp_in;
      int amp_in_y, amp_in_yprev;
      double amp_out;
      int amp_out_y, amp_out_yprev;
      String s_in = "in-wave";
      String s_out = "out-wave";
      String s_scalar_ln1 = "scalar";
      String s_scalar_ln2 = "(in-wave -";
      String s_scalar_ln3 = " out-wave)";

      // erase everything that was there before
      g.setColor(Color.white);
      g.fillRect(0, 0, width-1, height-1);

      amp_scalar_yprev = 0;
      amp_in_yprev = 0;
      amp_out_yprev = 0;
      for (x = 0; x < spacelen; x++) {
         // work out 1/r as a function of distance from the wavecenter
         if (x < wavecenterloc)
           r = (double) (wavecenterloc - x)/2; // the /2 spreads out the wave
         else
           r = (double) (x - wavecenterloc)/2;
         r = r * 0.25e-12;
         if (r != 0) {
           amp_out = (amp_max/r) * 
                 ((Math.cos(w*t)*Math.cos(k*r)+Math.sin(w*t)*Math.sin(k*r))/
                  (Math.cos(k*r)*Math.cos(k*r)+Math.sin(k*r)*Math.sin(k*r)));
           amp_in = (amp_max/r) * 
                 (Math.cos(w*t)*Math.cos(k*r)-Math.sin(w*t)*Math.sin(k*r));
           amp_scalar = amp_in - amp_out;

           // scale the wave's heights to fit the display
           amp_out_y = (int) (amp_out*15);
           amp_in_y = (int) (amp_in*15);
           amp_scalar_y = (int) (amp_scalar*15);

           if (first == 0) {
              // draw the out wave
              g.setColor(Color.green);
              g.drawLine(x-1, (int) base_y-amp_out_yprev, x, base_y-amp_out_y);
              g.setColor(Color.black);
              g.drawString(s_out, (spacelen/2)+17, base_y-15);
 
              // draw the in wave
              g.setColor(Color.red);
              g.drawLine(x-1, (int) 75+base_y-amp_in_yprev, x, 75+base_y-amp_in_y);
              g.setColor(Color.black);
              g.drawString(s_in, (spacelen/2)+17, 75+base_y-15);

              // draw the scalar/standing wave
              g.setColor(Color.black);
              g.drawLine(x-1, (int) 175+base_y-amp_scalar_yprev, x, 
                         175+base_y-amp_scalar_y);
              g.setColor(Color.black);
              g.drawString(s_scalar_ln1, (spacelen/2)+17, 175+base_y-45);
              g.drawString(s_scalar_ln2, (spacelen/2)+17, 175+base_y-30);
              g.drawString(s_scalar_ln3, (spacelen/2)+17, 175+base_y-15);
           }
           first = 0;
           amp_scalar_yprev = amp_scalar_y;
           amp_in_yprev = amp_in_y;
           amp_out_yprev = amp_out_y;
         }
      }
   }

Download the program code and experiment for yourself

The following is the full java program code written as a java applet along with a html file to run it with. To download, right-click on a file and choose Save As... or use whatever method you normally do.

Once you've downloaded the file called inout_wave_eqns_1d_src.txt change the name to inout_wave_eqns_1d_src.java (i.e. change .txt to .java.) This allows you to make modifications to the code and experiment yourself. The java compiler is available for free from Sun's java website (look for Java SE or the Java JDK.)

You can use the command line compiler or a full integrated development environment. The code is in the file called inout_wave_eqns_1d_src.java. To compile it from the command line, bring up a command line window and type:

javac inout_wave_eqns_1d_src.java

That creates a file called inout_wave_eqns_1d_src.class. Then bring up the other file available for download above, inout_wave_eqns_1d_src.htm, in a web browser. That runs the java applet (the .class file) in the browser... provided you also have the java runtime environment (JRE), also available for free from Sun's java website though if your operating system is recent you may already have it.

Warning: If you change the code, recompile, and just refresh your browser you won't get your new version (with Internet Explorer anyway.) You'll have to close your browser window and open a brand new one.

If you're not familiar with java or java applets and want to get up to speed very guickly, have a look at this Java Applet Tutorial by Michael McGuffin.