Derivation of the Relativistic Lorentz Transformation Using the Wave Structure of Matter - May 27, 2007
Abstract
The SRT frequency shift, time dilation and energy equivalence formulas are derived from wave structure of matter concepts. The derivation shown removes Einstein’s requirement for the constancy of the speed of light between reference frames, which is not necessary in producing the results of the Lorentz transforms. Also, the photon is revealed to be the interaction between two electron wave centers, not a separate particle, showing a preference for Tetrode’s concept of a photon.
I. Introduction
In 1842 Christian Doppler first published his theory of the Doppler effect [1], which has been exhaustively corroborated by experimental data for all situations with the exception of relativistic circumstances. Due to a notable deviation between experimental data and theoretical calculations in the field of electrodynamics of moving bodies, specifically the Michelson-Morley experiment by the turn of the 19th century, new ways of predicting wave shifts due to motion were required. To account for these inconsistencies, the work of Lorentz and Einstein, among others, led to Einstein’s special relativity theory (SRT). [2] This theory allowed for more accurate calculations of the Doppler shift of objects moving at relativistic speeds, but SRT posed more questions about how the world works than it answered.
This may be attributed partially to the belief in field theory, which is generally described as a result of fields that interact between particles. Due to the assumed discrete nature of a particle and the lack of a concrete definition of a field and its structural elements, the investigation of the electromagnetic waves from moving bodies was hindered by the lack of solid theoretical models with which to perform mathematical derivations. An intuitive guess was required on Einstein’s part about the constancy of the speed of light in all inertial reference frames, which turned out to be verified experimentally but with no underlying explanation for the cause. Although the first hypothesis in Einstein’s original paper [3] regarding the constancy of the speed of light between reference frames has been verified experimentally, his second hypothesis of relativity is still being challenged by many experiments, particularly the measurement of the Lorentz force due to a spinning magnet on a stationary charge. [4]
This paper will show a short and conceptually satisfying derivation that starts with classical, non-relativistic Doppler shift and applies the wave structure of matter (WSM) created by Milo Wolff. [5] The end result is the same equation produced by the Lorentz Transformation as Einstein predicted a century ago.
II. Relativistic Doppler shift and photons
Since the WSM theory describes a particle as a combination of an in-wave and an out-wave, [5] both waves will need to be classically Doppler shifted to see how the interaction brings about the effects predicted by SRT.
Let us assume that the wave-center being analyzed is moving towards the
observer, (the apparatus monitoring the incoming wave center.) The
out-waves from all matter in the universe have a speed of
 and are
classically Doppler shifted and combined using the Huygens principle to
become the in-wave at the wave center:
and are
classically Doppler shifted and combined using the Huygens principle to
become the in-wave at the wave center:
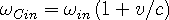 | (2a) |
and, the out-wave leaving the wave center at speed
 undergoes another
classical Doppler shift before reaching the observer:
undergoes another
classical Doppler shift before reaching the observer:
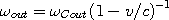 | (2b) |
where 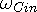 is
the frequency of the in-wave at the wave-center,
is
the frequency of the in-wave at the wave-center,
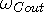 is the
frequency of the out-wave from the wave-center,
is the
frequency of the out-wave from the wave-center,
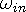 is the
frequency of the in-wave from the universe,
is the
frequency of the in-wave from the universe,
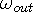 is the frequency of the out-wave as seen by the observer,
is the frequency of the out-wave as seen by the observer,
 is the
relative velocity between the observer and wave-center, and
is the
relative velocity between the observer and wave-center, and
 is the speed of light.
is the speed of light.
Knowing that the out-wave from a wave center is reflected from the
in-wave arriving at the wave center, we know that
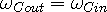 .
Then the in-wave frequency transfer function is:
.
Then the in-wave frequency transfer function is:
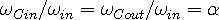 | (2c) |
while the out-wave frequency transfer function is:
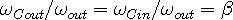 | (2d) |
To equate the in and out-waves of WSM in terms of photon frequency we use
Tetrode’s perception that the photon is produced by the combination of
waves from a sink and a source. In our example
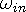 acts
as the source and
acts
as the source and 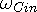 the sink for the input, while
the sink for the input, while 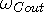 acts as the source and
acts as the source and 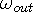 is the sink for the output. [6] This intermodulation of waves
is provided by the following two equations:
is the sink for the output. [6] This intermodulation of waves
is provided by the following two equations:
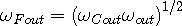 | (2e) |
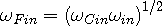 | (2f) |
where 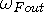 is
the photon frequency exhibited by the out-wave intermodulation, and
is
the photon frequency exhibited by the out-wave intermodulation, and
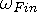 is the
frequency from the in-waves. An important thing to notice is that if the
observer and wave center are in the same reference frame,
is the
frequency from the in-waves. An important thing to notice is that if the
observer and wave center are in the same reference frame,
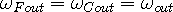 ,
which agrees with experimental results.
,
which agrees with experimental results.
The ratio of the in-wave transfer function, Eqn 2c, and that of the out-wave, Eqn 2d, at the observer is:
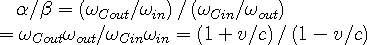 | (2g) |
which is the ratio of the product of out-wave frequencies to the product of in-wave frequencies.
To get the Eqn 2g in terms of the photon frequencies, substitute in Eqns 2e and 2f, and then rearrange to get the equation in terms of the photon frequency seen at the observer:
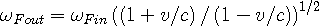 | (2h) |
This is the relativistic Doppler shift as accepted by modern physics. The assumption of the source moving towards the observer was made to show the reader where the classical Doppler shift equations came from, but with the opposite direction of motion the same results are reached.
This derivation shows that space acts as a stationary medium to any observer’s frame of reference, and the velocity term in Relativistic Doppler shift is due only to relative velocity between the source and the observer’s frame of reference. In fact, the nature of relativity requires an absolute reference frame by definition: SRT requires a constant speed of light, which implies an absolute reference. The constant speed of light (as seen from WSM) is derived from a fixed value of matter density within the Hubble sphere. [7] It also verifies Tetrode’s explanation of energy exchange and describes what a photon really is, as opposed to the wave-particle duality currently accepted by many physicists.
The results of this derivation also show that in-waves from the Hubble Sphere act like a timing circuit that provides the expected frequency from a wave center that is in the same reference frame as the observer. When the wave center is in a different reference frame, the classical Doppler shifts of the in and out-waves provide the relativistic frequency shift corroborated by experimental data over the past century.
III. Time dilation of bodies in motion
Time dilation is the apparent slowing of time of a relativistically moving body with respect to a body in a different reference frame. If we apply WSM and specifically the assumption that the in-waves from all matter in the universe is the timing circuit by which all interactions are measured, then expired time in a relativistically moving body is based on the mean frequency seen at the wave centers that make up this body.
The mean frequency seen by a wave center is given by:
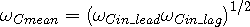 | (3a) |
where 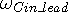 is the in-wave frequency seen at the side of the wave center in the
direction of motion, while
is the in-wave frequency seen at the side of the wave center in the
direction of motion, while 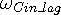 is the in-wave frequency seen at the side opposite the direction of motion.
is the in-wave frequency seen at the side opposite the direction of motion.
Using classical Doppler shift shown in Eqn 2a and the opposite shift for the lagging side, we find that the mean frequency for the moving body is:
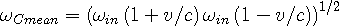 | (3b) |
If the body is at rest with respect to the observer, note that the mean frequency is given by:
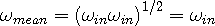 | (3c) |
Eqn 3b can be simplified by substituting in Eqn 3c to get:
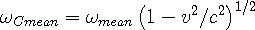 | (3d) |
Using this relationship and knowing that all events in a wave center are timed by the in-wave seen from the universe, (they are proportional,) time in an observer’s reference frame can be related to time in a moving reference frame by the following relation:
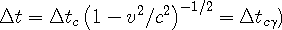 | (3e) |
where 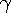 is the
result from the Lorentz Transforms,
is the
result from the Lorentz Transforms, 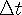 is the time passed from the observer’s reference frame, and
is the time passed from the observer’s reference frame, and
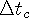 is the time passed in every wave center of the moving body’s reference frame.
is the time passed in every wave center of the moving body’s reference frame.
This is the time-dilation formula of SRT, which shows that time dilation is based on classical Doppler shift of the in-wave seen by a moving body. It also proves that the universe’s in-wave provides the timing for all events, since all matter is and all energy transfers come from wave centers, removing the mathematical possibility of time-travel drawn from previous derivations of SRT.
IV. Other equivalences in SRT
In the previous section, we have deduced that time is based on the mean frequency of the in-wave as seen in the reference frame. The wavelength of the in and out-waves is the measuring standard for length measurements in space, and wavelength is inversely proportional to frequency, so Eqn 3d can be used to show that the length contraction relation is:
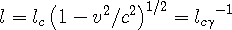 | (4a) |
where 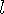 is the length as seen by an observer in a different reference frame, and
is the length as seen by an observer in a different reference frame, and
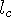 is the length
seen in the moving reference frame.
is the length
seen in the moving reference frame.
Since the WSM shows us that matter is simply waves, from a different reference frame, mass dilates equivalently to the mean frequency shift, also based on this same mean frequency dilation factor from Eqn 3d:
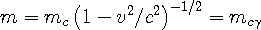 | (4b) |
where 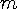 is the apparent mass of a moving body with respect to a stationary observer,
and
is the apparent mass of a moving body with respect to a stationary observer,
and 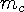 is the mass of
the body from the moving body’s reference frame.
is the mass of
the body from the moving body’s reference frame.
Using the WSM, Eqn 4b and the kinetic energy equation from classical mechanics, we find the kinetic energy of the in and out-waves of a moving wave center to be:
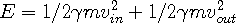 | (4c) |
where 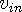 is the in-wave velocity,
is the in-wave velocity, 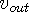 is the out-wave velocity, and
is the out-wave velocity, and
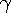 is based on
the relative velocity between the reference frames and is unrelated to the
speed of the in or out-waves.
is based on
the relative velocity between the reference frames and is unrelated to the
speed of the in or out-waves.
Since both waves travel at the wave speed of space,
 , and the out-wave
travels in the opposite direction as the in-wave:
, and the out-wave
travels in the opposite direction as the in-wave:
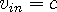 and and 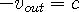 | (4d) |
Therefore Eqn 4c becomes:
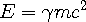 | (4e) |
which is Einstein’s famous energy equivalence equation. [3] This derivation shows that rest mass is really the kinetic energy of the in and out-waves of an object when the observer is stationary with respect to the object.
V. Implications of these derivations
These simple conceptual derivations take a lot of the mystery out of SRT by presenting WSM with explicit mechanisms that produce the same results as Einstein. The derivations are also further verification that the WSM is an important theory in that it ties together SRT and quantum mechanics (QM) with a physical model for matter and energy exchange that satisfies the requirements of both of these major fields of physics, without alienating any of the experimental proof that made both older theories so strong.
There are several examples in QM where the wave functions operate similarly as in this paper to produce the accurate results for which QM became famous. For example, a photon is created from the product of the wave functions in the case of photon transfer between two electrons and in the case of a collision of a positron and an electron.
Time dilation is simply the product of classical Doppler shift of the in-wave of a moving reference frame, which causes a change in the timing of atomic radiations and all other time-dependant processes. This model for time dilation conceptually removes any fantastical ideas about time travel from theoretical physics, which was already highly improbable since “we have not yet been overrun by tourists from the future.” [8]
This paper also separates Einstein’s second principle of SRT from the results of SRT, since the derivation provided in this paper does not require a constant speed of light in all reference frames.
This paper also shows that in and out-waves of wave centers travel at the wave speed for local space, but since the photon is the product of the intermodulation between the in and out-waves between wave centers, the photon itself is not restricted by this wave speed.
For more on SRT in the WSM, see the derivations by Milo Wolff [9] and by Denys Lépinard. [10] The derivation presented by Wolff uses the laws of conservation and symmetry to provide the physical origin of mass increase and Doppler shift, which does not require a constant speed of light. Lépinard uses the phase waves and wavelengths of WSM to produce the same results.
VI. Conclusion
This paper provides the same results as SRT using non-relativistic Doppler shifts, showing the direct correlation between classical and relativistic Doppler shifts. The WSM ties SRT and classical Doppler shifts together with a physical explanation that shows that the in-wave and out-wave are required concepts to unify the many separate fields of physics that have developed over the past century.
VII. References
| [1] | P. M. Schuster, Moving the Stars - Christian Doppler: His Life, His Works and Principle, and the World After, (Living Edition, Pollauberg, Austria, 2005). |
| [2] | A. Einstein, Relativity: The Special and the General Theory, (Three Rivers Press, New York, NY, 1961). |
| [3] | A. Einstein, “On the Electrodynamics of Moving Bodies”, Annalen der Physik 17, p. 891 (1905), http://web.mit.edu/8.033/einstein1905.pdf. |
| [4] | “Lorentz Force and Rotational Relativity”, Journal of Theoretics Comments Section, Oct.-Nov. 2004 - http://www.journaloftheoretics.com/Comments/c6-5.pdf. |
| [5] | M. Wolff, Exploring the Unknown Universe, 2ndEd., pp. 178-200, (Technotran Press, Manhattan Beach, CA, 1994). |
| [6] | H. Tetrode, “Uber den Wirkungszusammenhang der Welt: Eine Erweiterung der Klassischen Dynamik”, Zeitschrift fur Physik 10, pp. 317-328, (1922). |
| [7] | M. Harney, “The Cosmological-Redshift Explained by the Intersection of Hubble Spheres”, Aperion 13, p. 293 (2006), http://redshift.vif.com/JournalFiles/V13NO2PDF/V13N2HAR.pdf. |
| [8] | S. Hawking, The Illustrated A Brief History of Time, p. 206, (Bantam Books, New York, NY, 1996). |
| [9] | M. Wolff, “Relativistic Mass Increase and Doppler Shift Without Special Relativity”, Galilean Electrodynamics, pp. 117-120, (1998). |
| [10] | D. Lepinard, “Alteration of Matter in Motion”, (2005), http://www.ontostat.com/anglais/relativism_gb.htm. |